Graphing the Glissando in "Rhapsody in Blue"

George Gershwin's "Rhapsody in Blue" famously opens with a trilling clarinet that rockets up more than two octaves in what's known as a "glissando," in which an instrument's pitch bends across a span of notes in a continuous climb or descent rather than stopping at discrete frequencies. Here's an example from the Columbia Symphony Orchestra, which probably sounds familiar:

The modern score allows for two beats to span the interval at Molto moderato—a tempo of 80, so 2⅔ seconds—but the solo clarinetist is allowed the artistic liberty to draw out the bend, and more importantly, what path to take from the low F to the high B♭. (This is written as a low G to a double C in the score since the clarinet is tuned to B♭.)

In data visualization and UX terms, he or she can choose both the duration of the animation or "tween" and the "easing formula," or how quickly a moving object, say, gets from it's starting to final position. This is rarely a linear process with a fixed velocity. Picture how, say, when you click "next" on a slideshow carousel on a website, the next photo typically "snaps" into place, hurrying most of the way over and then easing to a stop at the very end (or sometimes even overshooting and correcting).

I've always wanted to compare different performances of the Rhapsody to see what those easing formulas look like. After playing around with about a dozen pitch-detection libraries, I put together this comparison of five glissandi from different renditions I found on YouTube:

As you can see, all but one of the principal clarinetists front-loaded the ascent to at least some extent and then glided smoothly into harbor. These most closely resembles the easePolyOut formula in D3, though the curves you see here are not nearly as clean—nor should they be.

This may have to do with the mechanics of bending a pitch, which is easier on a reed instrument than on brass—though this guy pulls it off masterfully on a piccolo trumpet. Miles Davis also bends a short distance in the opening passage of "My Funny Valentine" in his Live at the Lincoln Center performance in 1964. (If you don't own that album, which features Herbie Hancock, Ron Carter, Tony Williams, and George Coleman, buy it immediately.)

Curiously, the original score for the 1924 debut of "Rhapsody in Blue" does not specify a glissando:

But a grainy recording of that performance—which was allegedly attended by Sergei Rachmaninoff—suggests it was always part of Gershwin's vision. The orchestration was finished at the last minute, to the point that, at least according to lore, "The work’s significant piano solo was incomplete in this hasty arrangement. [...] At one point, a full page of blank sheet music was inserted in place of a piano solo, with a note for the conductor to 'wait for [Gershwin’s] nod'– when George would signal the band at the end of his solo."

Calculating Pitches

I went into this diversion knowing nothing about how audio is encoded and came out knowing just a little bit. Any given note in a musical recording has many different frequencies—known as "overtones"—which are responsible for the timbre. This is why a clarinet and a trumpet can play the same note but sound distinctly different.

Distinguishing the fundamental frequency from the overtones is not simple. There are several different algorithms that attempt this with varying success. The most sophisticated open-source library I found is called "aubio", which is written in C but has a well-documented Python wrapper.

You can see my tests of each algorithm in the "Test Pitch Detection" Python notebook in the repo. The best, by far, is the default algorithm, called "yinfft," which gets most of the notes in a given recording correct. For example, here's what it returns for the glissando from the Columbia Symphony Orchestra when you split it up into little pieces that are about 0.23 seconds each. (WAV files typically have 44,100 frames per second, which the code evaluates in chunks of 1024).

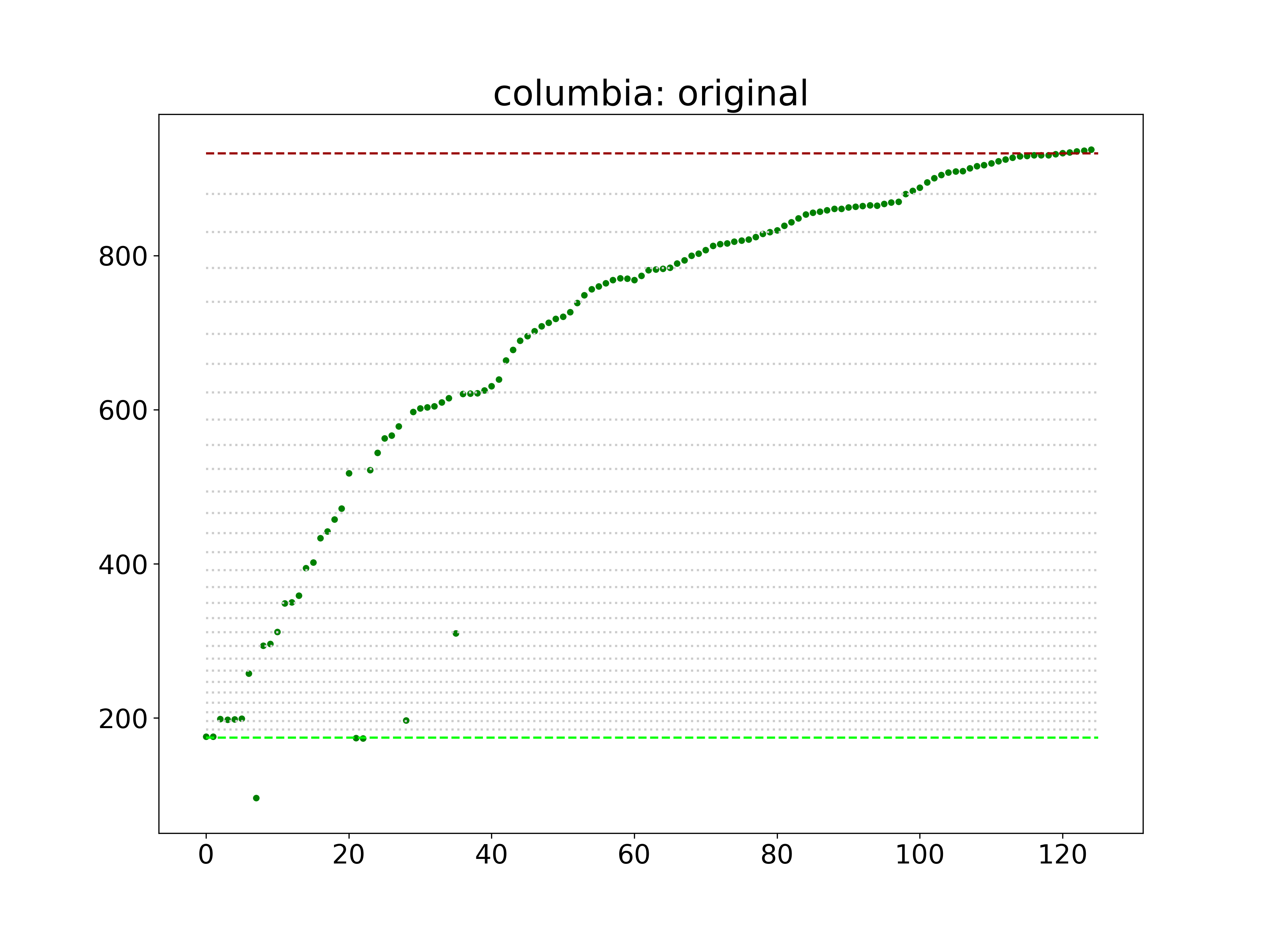
The basic shape is intact, but there are several outliers. To remedy this, I wrote a simple algorithm to guess the appropriate frequency of any note significantly distant from its neighbors, which is detailed in the README. It's not perfect, but it reins in the mistakes reasonably well without overfitting the curve too much. By all means, feel free to hack on it and send me a pull request.

Postscript

You may be wondering about that fifth clarinest who takes the longest and most deliberate route to the top. That is from a performance here in Washington, D.C. by the National Symphony Orchestra on January 22, 2017, two days after former President Trump's inauguration. The soloist climbs almost stepwise until the very end, as if he didn't ever want the glissando to end. I was there. None of us did.