Pascal's Triangle as a Galton Box

There's a wonderful math toy known as a "bean machine" or "Galton board" that demonstrates normal distributions though a simple mechanism: A large number of small metal balls—or beans, if you prefer—are fed through an staggered lattice of metal pegs, which, when the ball collides with the peg, causes it to drop either to the left or the right. Here's a simple demonstration from Wikipedia.

The way it works is pretty self-evident: The beans have a 50% chance of dropping to the left or the right when they strike a peg, leading them to the next peg, where they again drop left or right. Naturally, only a small number drop left every time, or right every time, while most reach a final point closer to the center, though not always by the same path.

I was working on a project recently that involved the coefficients of Pascal's Triangle, and I noticed something interesting about the numbers: Each one represents the total number of unique paths that a dropping ball could take from the top of the triangle to the bottom. Here's a crude sketch I made:

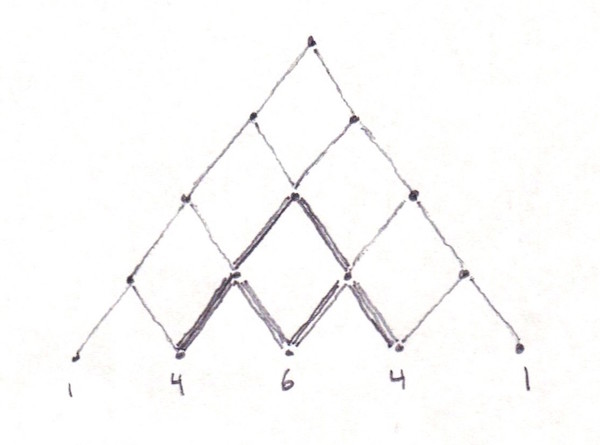
That reminded me of Galton boards—which, as of this writing, cost over $1,000 on Amazon if you want your own—and how they might be able to create Pascal's Triangle. Instead of shelling out $1,000, I ginned up a simulator, taking one little liberty: I coded it so that every pair of beans that strike a peg fall once to the left and once to the right, so that every possible path through the pegs is reached one time. The floor of the machine—the red bar—moves down after each row is completed. The beans always fall to the left first, so the paths are traveled in order.

As you see, when you sum the number of times each terminal node is reached by one of the possible paths, you get Pascal's Triangle!